Heat Pump Ethics Problem

Introduction

Engineering Background

Engineering Problem

Ethical Problem

Questions on Ethics and Professionalism

Engineering Solution

Ethical Solution

Introduction

You are a engineer at a HVAC/energy consulting company in your area. Your responsibility is to design and purchase equipment for projects that you work on. You are involved in various new and retrofit projects in the community, involving commercial buildings, schools, residential houses and industrial buildings. You are required to have a knowledge of thermodynamics, heat transfer, HVAC, energy conservation and energy conversion devices such as heat pumps.

The particular project under consideration involves the design of a new 200-room motel in your city. The architect has completed the floor plan design and overall geometry of the buildings. Now you must design specifications for the rooms' heating and cooling systems and contract the systems from equipment wholesalers in the area. You have calculated that each has about the same heating load of 20,000 Btu/hr. Several suppliers have bid on your job. You notice that one suppliers has bid the equipment at about 20% below the average price of all the other suppliers. Although you realize that because you are buying such a large number of heat pumps you can obtain a competitive price advantage, this supplier's price seems too good to be true.

This supplier visits you the following week to discuss his bid on the heat pumps. You inquire about his low bid on the heat pumps and ask to see some performance data on his units. He provides you with engineering data.

Back to Top

Engineering Background

The supplier gives you technical performance data on his Slick Brand heat pumps. The following information is provided at the design operating conditions:

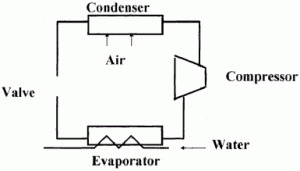
Condenser: Air flow rate = 750 CFM Inlet temperature = 60 °F Outlet temperature = 85 °F

Evaporator: Water flow rate = 2.6 GPM Water inlet temperature = 52 °F Water outlet temperature = 42 °F

Compressor: Current draw = 8 amps

Other information:

The system is operated at 120 V line voltage.

Figure 1. Heat Pump Schematic

Back to Top

Engineering Problem

You are suspicious of this salesman. What would you do to verify your concerns?

Back to Top

Ethical Problem

Suppose you learn that the data on the heat pump is in error. You confront the salesman. He tells you that he is sorry that he made a mistake. The current draw on the compressor should be higher. He says that he really wants to sell this batch of heat pumps because they use CFC 22 and the refrigerant will be phased out soon. He says that he wants to make you a "deal" and sell this batch of heat pumps at not just 20% off but now 50% lower than similar units on the market.

What do you do?

Back to Top

Questions on Ethics and Professionalism

1. What are the relevant facts for this case?
2. Are there any unknown relevant facts?
3. Are there any conflicts in this problem?
4. What are the consequences of the possible solutions?
5. Design alternate solutions to present to your engineering manager.
6. What should you do?

Back to Top

Engineering Solution

Assumptions:

• Constant Specific Heat of water
• Density of air = 0.075 Ib/ft³

1. How would you confirm or deny the salesman's claims about the heat pump?

An energy balance on the heat pump in the heating mode can be performed as follows:

Condenser:

• Air flow rate = 750 CFM Inlet temperature = 60 °F
• Outlet temperature = 85 °F
• Qcond= mC(T_Out T_in) = 750 CFM(0.0751b/ft³)0.24btu/lbF(8560)F(60min/hr) = 20,250 btu/hr

Evaporator:

• Water flow rate = 2.6 GPM
• Water inlet temperature = 52 °F
• Water outlet temperature = 42 °F
• Qevap = mc(T_in T_Out) = 2.6gal/min(8.3 lb/gal)(lbtu/lbR)(5242)F(60min/hr) = 13,000 btu/hr (with round off)

Compressor:

Current draw = 8 amps

The power input from the compressor is roughly:

Power = volts x amps (neglecting the power factor) = 120 volts x 8 amps = 960 watts = 3276 btu/hr

Note that the input from the evaporator (13,000 btu/hr) plus the compressor work (3275 btu/hr) is not equal to the heat given off from the condenser(20,250 btu/hr). Something is wrong thermodynamically!

Note also that the COP)_h of this unit is not reasonable with a value of

C0P)_h = Q_cond/Power = 20,250/3275 = 6.2. This is much too high.

Typical values of COP for heat pumps are 2 3.

Back to Top

Ethical Solution

1. What are the relevant facts for this case?
   1. The heat pump product information is in error! An energy balance on the heat pump reveals this fact. See above solution. B. You need to buy 200 heat pumps. C. The supplier has a very good price on heat pumps! D. You could save a lot of money on the initial cost of his heat pumps. E. His units use a CFC.
2. Are there any unknown relevant facts?
   1. Is the supplier violating any federal regulations such as the DOE energy rating standards for heat pumps? All appliances are required to have an energy rating such as EER (in Btu/watt-hr) posted on such devices. EER greater than 13 is extremely rare. The EER is about 21 for the product information given on this heat pump.
   2. Are his heat pumps reliable? Will they break down in 3 years?
   3. What will be the operating cost of these units? Will they use more electricity than comparable units?
   4. Is the supplier reliable?
3. Are their any conflicts in this problem?
   1. Should you choose the lower-priced units rather than buy other higher-priced units that do not have questionable performance? (price vs. performance)
   2. Should you purchase the lower-priced units knowing that may produce some potential CFC emission problems? How will the CFCs be dealt with? With they be recycled? What happens if the EPA bans the use of CFCs?

4. Does it violate any professional codes (e.g. NSPE)?

   The NSPE Code of Ethics of Engineers states:

   1.b. "Engineers shall approve only those engineering documents which are safe for public health, property and welfare in conformity with accepted standards."

   "Accepted standards" here could refer to the DOE Energy Standards. The engineer should not approve any documents in which the questionable heat pumps are used.

   1.c. "Engineers shall not reveal facts, data or information obtained in a professional capacity with the prior consent of the client or employer except as authorized or required by law or this Code."

   Section 1 .d. says; "Engineers shall not permit the use of their name or firm name nor associate in business ventures with any person or firm which they have reason to believe is engaging in fraudulent or dishonest business or professional practices."

5. What are the consequences of the possible solutions?
   1. Using the CFC heat pumps may cause pollution/recycling problems but you may save a lot of money on the initial cost (though the users may have problems with reliability and operational costs).
   2. Should you check to see if you should have the supplier investigated in case his company has violated some DOE regulations?

6. Design alternate solutions to present to your engineering manager.

   The engineer may be able to suggest that the supplier's heat pumps be tested by DOE to obtain a correct rating. However the company may not want to do this because this will cost money and the company may be fined for having an incorrect rating on the units.

7. What should you do?

   You should probably not use the units without certification and without checking the performance of the units. You are apt to have future problems with reliability and performance if this is not done.

   You must also provide a way to guarantee a supply of refrigerant CFC 22 in the future or these units will be of no use when they leak refrigerant sooner or later.

Back to Top