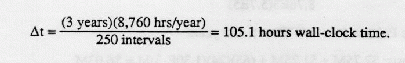Probabilistic Software Testing

Introduction

Questions

Solutions

Introduction

Because it is impossible to deterministically (100%) test the software of the Mark-5 aircraft controller, a probabilistic test (WHIZ) is developed. WHIZ owes its savings in test time to probabilistic analysis. It costs $2.75M to develop and install WHIZ. WHIZ takes 89 days (24 hours/day) to completely test a Mark-5, at a cost of $1,200/hour. The extraordinary gain in speed results from not testing all possible states of the Mark-5 system. Moreover, when bugs are fixed, WHIZ may be resumed from the execution-point where the bug was detected, rather than restarting at time-zero as in the "brute force" (deterministic) method.

It is estimated at >99% confidence (one-sided lower bound) that after WHIZ-testing, the undetected bugs remaining in the Mark-5 (mean time to fault) of 1.0E5 years. A software fault is assumed to cause a failure such that with unit probability (p = 1), a fatal crash of the host airplane will occur. Without WHIZ-testing it is estimated at >99% confidence (one-sided lower bound) that the MTTF is 95 years, based on existing in-house probabilistic tests.

An airplane crash is presumed to cause 350 deaths at $1.25M per death in settlement costs, plus $490M in loss of aircraft and related expenses. The on-board fright recorder is assumed to unfailingly (p = 1) establish the Mark-5 as the cause of the crash when it has in fact failed. In this case, Wondrous Avionics, Inc., manufacturers and distributors of the Mark-5, will incur all costs due to the crash. (Product liability insurance is not feasible.)

Assume that the installed base for the Mark-5 will "ramp" linearly from zero to 250 installed units in three years. Assume that each Mark-5 is vulnerable to causing an airplane crash for 11 hours of each calendar day, and that the process is Poisson. Ignore the time-value (rate of return) of capital in the economic analysis. Assume that WHIZ development and testing costs must be absorbed solely by Wondrous Avionics, Inc.

If WHIZ is used, it is done as a qualifying test. That is, only one Mark-5 system is tested with WHIZ. In the problems below, only the software is under consideration. Assume that the hardware and firmware may be analyzed separately.

Back to Top

Questions

(a) Based solely on economic analysis. and relative to the in-house test, is WHIZ-testing economically justified?

(b) If not economically justified in (a), and assuming the linear "ramp" continues indefinitely, how many units must be installed to make WHIZ-testing economically justified?

(c) Ignore part (b) in this problem, and consider part (a) and the information supplied relevant to it.

A modification, WHIZ M2, will cut test time to 65 days and raise the MTTF to 5.70E5 years at >99% confidence (one-sided lower bound). WHIZM2 will cost $1.25M to implement (in addition to the $2.75M development cost of WHIZ), and will cost $1300 per hour to run. Assume WHIZ M2 development will not delay shipment of the Mark-5. All WHIZ and WH1Z M2 costs must be absorbed by Wondrous Avionics, Inc.

If WHIZM2 is used, it is done as a qualifying test. Only one Mark-5 system will be tested with WHIZ M2. Based solely on economic analysis, relative to the in-house test and the WHIZ-test, is WHIZ M2-testing justified?

(d) Comment on the ethical implications of the above scenarios. Is it ethically justifiable to place a dollar value on human life? If so, how should it be computed? In not, how should engineers and society determine the acceptable risk of a particular technology?

Is it ethically justifiable that wondrous Avionics, Inc. absorb all testing costs? Should other entities share these costs? Who? Why? When?

(e) Comment on the relevance of the principle of informed consent as it may relate to the scenarios above. If informed consent is to be invoked, devise a separate plan for so doing where the consent is to be obtained from individually from each of these groups:

1. The airplane manufacturer
2. The airplane owner and/or operator
3. The airplane crew
4. The airplane's passengers.

(f) Discuss the practicalities of each of the plans outlined in part (e).

Note: Software testing and maintenance is an extremely complex matter! In the much-simplified treatment above we have attempted to make the problems tractable in the classroom.

Students should be aware that maintenance of software inevitably means revisions to the code and thus retesting. The above problems focus exclusively on software reliability, where in fact hardware and firmware must be included in a reliability assessment. And the action of removing one software bug may generate additional bugs such that the net effect would be an increase in bugs! The development of WHIZ and WHIZ M2 would also involve reliability testing.

Back to Top

Solutions

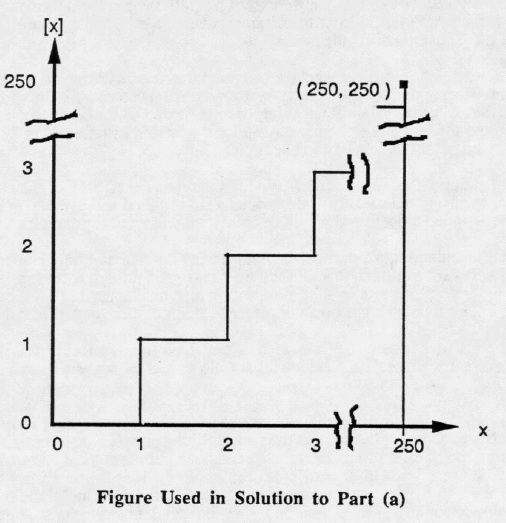
(a) Unlike hardware, software does not degenerate when not operating. (Hardware "ages" and "wears," even when on the shelf.) Therefore, operating time, not wall-clock time, is used in calculations. The Poisson model will be applied here. The figure below shows the build up of deployed M^-5 units. The operating hours are found by noting that a Mark-5 is added to the installed tease each t of wall clock time, where:

Then Δ t = (11/24) Δ t = (0.4583)(105.1) = 48.2 hours operating time. We may use the bracket function shown in the figure, or approximate it with a triangle. The sum of the operating hours is then:

The integral formula used above may be derived from consideration of the nature of the bracket function, "the greatest integer in x." (For non-integer upper limit a different formula results. You may derive it as a homework problem.) For large values of x, one may approximate the integral by the area of a triangle, ignoring the "staircase" shape. Here the error appears in the fourth significant figure. Operating time is the parameter used with MTTF in the Poisson model

Analysis of case with WHIZ

The Poisson model applies, and the parameter of interest is the ratio of operating time to MTTF (in hours): (l.50E6/8.76E3(1.0E5)) = 1.7E-3

This is the mean of the Poisson for a MTTF of l.OE5 years.

The expected loss is then: L = (1.7E-3)[(350)(1.25M) + 490M] = $1.59M.

The development and testing costs are: S = $2.75M + $1.20M(E-3)[(89)(24) = $5.31M

Total cost is: $1.59M + $5.31M = $6.90 M, cost w/ WHIZ.

Analysis of case without WHIZ

The Poisson mean is: (l.50E6/8.76E3(95)) = 1.80

This is the mean of the Poisson for a MTTF of 95 years.

The expected loss is then: L = (l.8o)t(3so)(l.25M) + 490M] = ($1.67E3)M, cost w/o WHIZ.

Clearly, the use of WHIZ is justified. The ratio of costs w/o WHIZ to w/WHIZ is 242. Note as well that the results may be sensitive to the study period used.

(b) As WHIZ is justified, the problem is not relevant. If such were not the case, one would equate the costs of not using WHIZ to the costs with WHIZ, using wall clock time as a variable expressed as a function of operating hours, as developed above. Solving for the variable thus yields the break-even point for WHIZ vs. non-WHIZ.

(c) The Poisson mean is: (1.50E6/8.76E3(5.7E5) = 3.00E-4

This is the mean of the Poisson for a MTIP of 5.7E5 years.

WHIZ M2 in-house costs: $2.75M + $1.25M + (65)(24)(1.30E-3)M =$6.03M

Expected loss: (3.00E-4)[(350)(1.25M) + 490M] = $0.278M

Total cost: $6.03M + $0.28M = $6.31M, cost with WHIZM2. Because WHIZ incurs costs of $6.90M, the use of WHIZ M2 is justified.

(d) By now it should be clear that the world is probabilistic, not deterministic. Hence, no technology (or anything else) is "100% safe" or certain.

A suggested acceptable risk level for humans in the USA, based in part on the work of Starr and others, is lE-9 per hour of exposure.Starr, C. "Social Benefit versus Technological Risk." Symposium on Human Ecology. Warrenton, VA, November 24 - 27, 1968. Also in Science, vol. 165, 1969: 1232 - 1238.Wujek, J. "An Upper Bound for Passenger Fatality Risk for the MARTA Rail Rapid Transit System." Desk Notes, 10 May 1974. This is of the same order as the risk encountered from natural cataclysms; floods, lightning strikes, and fires (USA data). Taking the reciprocal of this, and converting to years, we compute that the MTIP is about 1E5 years, consistent with the hypothetical Mark5 with WHIZ or WHIZ M2 testing in the problem.

Consider the cost of testing. Since some of a nation's citizens (but not all) benefit from the Mark-5, perhaps it is appropriate to assign some of the testing cost to the government. Perhaps a surtax on flights using the Mark-5 is appropriate, if the customer is made aware.

Consider that Wondrous Avionics, Inc., the airplane manufacturer, and the airline, profit. But these organizations pay taxes (if operated by a business, not government) so there is in some sense double-costing if they bear all the test costs. Should not safety-testing be part of the cost of doing business? The airplane manufacturer and the airline are already paying for the testing, as reflected in WAI's price to the airplane manufacturer, who passes on this cost to the airplane buyer.

(e) See Answers below:

• (el, e2) Test data and calculations are part of the engineering documentation. The buyer's engineers should have access to software test data, just as they may reasonably claim access to any test data of a product they evaluating. Trade secrets can be protected while disclosing MTTF data to the airplane manufacturer and the airplane owner and/or operator. Interpretation of these data is part of disclosure.
• (e3, e4) The airplane crew, because they are at risk and have responsibility for the safety of the passengers, have an ethical right to these data. Obviously, it follows that passengers have a right to know the risks attendant upon flying.

(f) Disclosure of test data to the airplane manufacturer and the airplane owner and/or operator was discussed in (el, e2) above. Communications to the crew and passengers is less straightforward. If test results confirm that using the Mark-5 produces no more risk than similar control systems already in place in the industry, it may be argued that informed consent is implied. This follows from the awareness of airplane crashes brought about by the news media (though not always accurately), and by investigation by an independent authority. Thus, it is argued, one is at least aware of some risk when aboard an airplane, in an automobile, etc. Communicating risk to the potential passengers is even more difficult, as discussed in part (g).

(g) Disclosure of risk is diametrically opposed to advertising. Even when the hazard may have been demonstrated to be extremely small, it is non-zero and points up the unpleasantness which is anathema to advertisers!

A class exercise, in which students are asked to give a brief oral presentation of risk before a mock public audience, may be useful. Consider doing so interactively, with coaching from the audience. The better coaches could exchange places with the speaker in a style of impromptu theater. Perhaps a reasoned response to part (g) would be a discussion of restraint in advertising. The codes of ethics of engineering societies demand as much, though advertising is not mentioned explicitly. For example, the IEEE Code of Ethics charges members: "...to disclose promptly factors that might endanger the public or the environment," and "...to be honest and realistic in stating claims or estimates based on available data ..." Airlines rarely mention safety in their ads, though it is implied and it is a reasonable expectation.

Back to Top