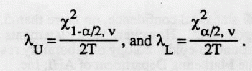Product Reliability, Hazard, and Risk

Author(s): Dr. Joseph H. Wujek, P.E.

Introduction

Solutions

Introduction

You work for Ajax Health Instruments, Inc. Ajax is developing an implantable patient-monitoring device. The device is implemented on a single-chip: Chip X. The user ("patient") may download health data by telephone to the hospital. Any mode of failure of this memory chip can be extremely hazardous to the patient because of incorrect data, data loss, and unknown or unidentified hazards. Most of the patients using the implant are over 50 years of age.

Field data for Chip X, under environmental stress conditions similar to Ajax's intended use, show six failures in 1.77 million part-hours. From this, a colleague has computed the point-estimate of the failure rate:

Under the robust assumption of constant failure rate, the Mean Time To F (m) is the reciprocal of failure rate, so: m = 2.95 (10⁵) hours.

Upon seeing this result, the Chief Engineer exclaims, "Wow, that's wonderful! The instrument operates continuously, so that's 8,760 hours per year. So on average we can operate our unit without failures from the part for 34 years!"

1. What fraction of installed Chip X can be expected to fail after 1 year?
2. If failure of Chip X results in patient death one out of three times, what is the probability of death due to Chip X failure of one or more patients after 2 years? Assume that the entire patient population had the device installed at the same time, and that no other patient fatalities occur in the 2-year interval.
3. Compute the two-sided 60% confidence limits (lower 20%, upper 80%) of failure rate.
4. Repeat (c) for two-sided confidence limits of: 80%, 90%, and 95%.
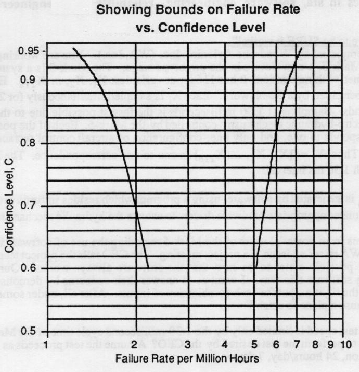
5. On semi-log paper carefully plot the results of (c) and (d). Use failure rate as the variable of the log-axis.
6. Repeat part (a) but now using the upper 90% one-sided confidence limit of failure rate.
7. The Marketing Department of Ajax wants to run an ad in journals read by physicians. They intend to show prominently: "Reliability of 34 years!" Comment on this. Consider in your comments how the ethics code of one or more engineering societies may be invoked.
8. Is Chip X suitable for the intended application? What considerations should be evaluated, and how?

Back to Top

Solutions

1. For constant failure rate, the fraction survived as a function of time is: R(t) = 1 - exp(-λ t), with λ =3.39E-6, and t = (24 operating hr/day)(365days/yr) = 8,760 hours. The fraction failed, F(t) = 1 - R(t) =1-R(8,760)=1 - 0.971 = 0.0290 (to 3 significant figures)
2. 1 - R(17,520) = 1 - 0.94234 = 0.0577 This is the fraction failed after 2 years. If 1/3 of the failures result in patient death, the probability of death due to Chip X failure is: P = (1/3)(0.0577) = 0.0192. The failure-rate is Chi-square distributed. The upper and lower bounds of failure rate are given by:
   

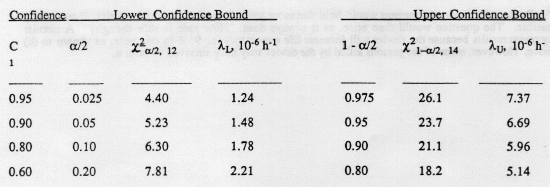
   In the above, T is the accumulated unit-hours of test; and x² indicates the Chi-square statistic at a given (two-sided) Confidence Level (1 - α / 2) or Significance (α / 2); with v degrees of freedom. For a failure truncated test, take v = 2f, where f is the number of failures. If the test is time-truncated, use v = 2( f + 1) for computing the upper bound, λ_u, and v = 2f for computing the lower bound, λ_L. The Chi-square statistic is tabulated in many statistics books and handbooks. For the problem at hand, T = 1.77E6 hours, f = 6. Lacking further information, assume that the test was time-terminated. This is typical of field data, where failures are noted but the equipment is repaired and continues to operate.

3. The solution is tabulated below.
4. The solution is tabulated below.
   
5. See plot below.
6. For one-sided confidence C:
   

   This result may be interpreted thus: "If we ran an infinite number of tests, 90% of the tests would yield a failure rate < 5.96E-6 per hour."

7. The intended ad is misleading. At 34 years, using the point estimate (50% confidence) for the MTBF (34 years), 63% of the chips will have failed!

   A more truthful statement is: "At 90% statistical confidence, no more than 5.1% of the chips used in our device will fail after one year of operation." However, such statements are not well understood by physicians unless they have a background in epidemiology or laboratory research. Further, it is "scary" and likely would not be accepted by the Marketing Department of AHI, Inc.

8. Chip X, based on data analyzed here, is not suitable for this application without additional safeguards. The loss of 5% of the chips after one year's operation is not acceptable, based on common hazards encountered daily such as driving an automobile, etc.
   

Back to Top

These problems were originally developed as part of an NSF-funded project to create numerical problems that raise ethical issues for use in engineering and other course assignments. The problems presented here have been edited slightly for clarity.

Return to Numerical & Design Problems With Ethical Content.