Challenger O-Ring Data Analysis

Introduction

Solutions

Footnotes

Introduction

The events leading to the Challenger disaster are well known. This problem involves analysis of O-ring data and involves arguing for a launch scrub based on the results.

The data of Table 1 have been used by David Hodges in the Freshman Seminar at University of California at Berkeley. 1 These data are from successful flights. Roger Boisjoly has indicated that these data were not available prior to the Challenger disaster.2 Use the data in Table 1 as needed.3

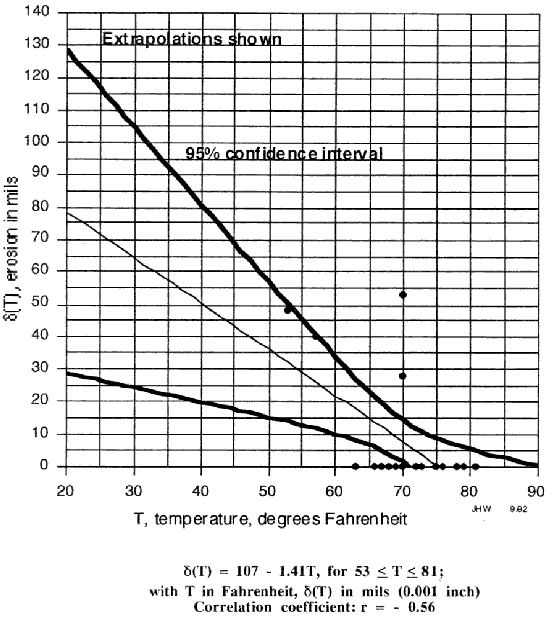
1. Obtain a linear regression plot and extrapolate the result to predict the material loss in the O-ring at the time of the disastrous Challenger launch. Assume that the O-ring was at the launch pad ambient temperature, 29 °F.
   1. Compute the correlation coefficient, r. Compare it the critical value of r at the 5% significance level and explain the meaning.
   2. Comment on the meaning of r, r², and 1 r². How relevant would this be in arguing for no launch?
   3. Compute the 95% confidence interval bounds and show the result in your linear plot.
   4. Comment on goodness of fit using the Chi-square test.
   5. Comment on goodness of fit using the Kolmogorov-Smirnov test.

      Table 1, Data from Challenger Post-flight Measurements3

      O-ring temp in °F	Erosion depth,δ mils *
      66.0	0.0
      70.0	53.0
      69.0	0.0
      68.0	0.0
      67.0	0.0
      72.0	0.0
      73.0	0.0
      70.0	0.0
      57.0	40.0
      63.0	0.0
      70.0	28.0
      78.0	0.0
      67.0	0.0
      53.0	48.0
      67.0	0.0
      75.0	0.0
      70.0	0.0
      81.0	0.0
      76.0	0.0
      79.0	0.0
      75.0	0.0
      76.0	0.0

      * 1 mil is 10^-3 inch

2. Try fitting polynomials of n = 2, 3, ... to the data and apply the measures of problem l(c), (d), and (e) to the results.
3. Try transforming the dataset by logarithmic or power functions and fit a linear function to the transformed variables. Apply the measures of problem 1(c), (d), and (e) to the results and compare.
4. For the results found above, how useful would the data have been in arguing for a "no launch" decision? Comment on the ethical implications.

Back to Top

Solutions

It is assumed that students have received instruction on the engineering aspects of the disaster.

The purpose of these exercises is to sensitize students to the following issues:

• The world is probabilistic, not deterministic, and nothing is "sure."
• Though data may be inconclusive, when matters of life and property are at stake, "not knowing" should be equivalent to "we have a problem."
• Linear regression is but one way of fitting a function to data and interpreting results statistically.

1. (The plot is given below, and is suitable for creating an overhead foil.) (Three significant figures are given in the equation for checking results.) At 29 °F the material loss (95 % confidence) is in the range of 25 to 105 mils. This extreme variability indicates (see also below) high risk of seal failure. Though extrapolation is always suspect, the very notion of "not knowing" with statistical validity how the seal would perform at 29 °F should have been taken as sufficient reason to cancel the launch.
   1. From Figure 1, r = ` 0.56. From a table of critical values of correlation coefficients, at the 95 % confidence level (5% significance, for 20 degrees of freedom [22 data pairs minus two parameters in the linear equation], r_c = 0.423 is found. 4. This means that with 5% probability, data exhibiting a correlation coefficient as great as 0.423 will not be correlated. Or, r_c may be interpreted as the maximum value that may take by chance (95% of the time) alone, when no correlation exists.
   2. The correlation coefficient r is defined thus: r= S_XY/(S_XS_Y)

      The numerator is the sample covariance, the denominator the product of the sample variances of the two variables: X, Y.

      Thus the r-value is a measure of association of the two variables. Now 0 < (absolute value) r < 1, with r = +/- 1 indicating perfect correlation, and r = 0 indicating perfect non-correlation. Then r² is a measure of the variability due to causality, and 1`r² is a measure of variability due to randomness. See also the comments just after the problem statement, above.

   3. See Figure 1. Explain the meaning of the confidence interval. One interpretation is: "If we performed a very large number of tests, 95% of the outcomes would lie in the indicated 95%`bounded range."
   4. For both the Chi-square test and the K-S test of problem (e) the test hypothesis is: H_o The data are uncorrelated.

      We accept the hypothesis if: X²_o> X²_{1 - α,v}

      where 1 `α= C is the confidence level (α is the significance level), and v is the degrees of freedom Here, v = N ` 1 ` m, where N is the number of observations of the variables (22 in this case), and m is the number of parameters in the equation being tested (m = 2 for linear equation).

      The term on the left side of the inequality is the observed Chi-square statistic, computed the data. The right side of the inequality is the value of the Chi-square variable corresponding to probability C, i.e. the value of the integral of the density function to the variate. These are tabulated.

      For the problem at hand:5 X²_0.95,19 = 30.1 and X²₀ = 422.

      Therefore, the hypothesis is accepted that the data are not linearly correlated.

   5. For the Kolmogorov-Smirnov test we use the same hypothesis: H_o The data are uncorrelated.

      We reject the hypothesis if: Sup{ y_f Y_d}?d_α(v)

      The subscripts on y refer to "fused" and "data" values, respectively. Thus, for a datapair x_d, Y_d the value of the fitted function at x_d is y_f . The maximum value ("supremum") is the compared to the K`S statistic for the significance level and degrees of freedom as in problem (d)6.

      We find Sup{|y_f y_d|} = 45, and d_0.05(l9) = 0.301, so we cannot reject the hypothesis that the data are not linearly correlated.

2. Problem 2 is intended for exercises in curve-fitting. Because of their open-ended nature, solutions are not given. A pitfall of using a logarithmic transformation is attempting to compute the logarithm of zero!
3. Problem 3 is intended for exercises in curve-fitting. Because of their open-ended nature, solutions are not given. A pitfall of using a logarithmic transformation is attempting to compute the logarithm of zero!
4. The erratic data would have been sufficient to indicate "we have a problem" because of the risk to human lives. The astronauts were not informed of the history of the O-ring defects, thus informed consent was not possible.

Back to Top

Footnotes

• 1. Lighthall, F. "Launching the Space Shuttle Challenger: Disciplinary Deficiencies in the Analysis of Engineering Data," IEEE Transactions on Engineering Management, Vol. 38, No. 1, February 1991. pp. 63-74.
• 2. Boisjoly, R. Pers. comm. November 1993.
• 3. Lighthall, p. 70, Table I.
• 4. Found in many texts and handbooks. See for example, Fisher, R., and Yates, F., Statistical Tables for Biological. Agricultural, and Medical Research. Oliver & Boyd, Ltd., Edinburgh, 1957.
• 5. Owen, D. Handbook of Statistical Tables. Addison`Wesley, Reading, MA, 1962. p. 51.
• 6. Owen, p. 64.
  

  Figure 1, Chart- Linear Regression on O-ring Data (After Lighthall)

Back to Top