Risk, Tradeoffs, and Informed Consent: "The Hundred-Year Flood"

Introduction

Solutions

Introduction

Recently, the 100-year flood plain (hereafter referred to as the "flood plain") for the Zilch River has been estimated by the state's waterway engineers. The estimates are based on historical records such as weather data, newspaper accounts, and interviews with long-time residents of communities along the river's course. Hydrology experts reviewed the report documenting the results and then it was made accessible for public comment. The final version of the report has been accepted by all interested parties as presenting a valid model. Consider a plot of land, Plot X, within the flood plain. Plot X is under consideration by Acme Oil Refiners as a site for an oil refinery. It is particularly attractive because ocean-going tankers have access to the site, and the closest city, Valhalla, has an ample supply of workers to construct and operate the proposed plant. The region is economically depressed and local government entities, civic organizations, and others have pursued Acme to build the plant at Plot X. The state and local governments have offered Acme attractive incentives to locate the plant in Plot X. For example, Acme could purchase the plant site for $1. Other incentives include: installation of utilities, access roads, and other infrastructure at no cost to Acme; no taxes assessed for the first ten years after start of operation, with low tax rates thereafter; and assistance in training workers from the start of construction planning through the completion of start-up. Acme top management persons consider this to be a "sweetheart deal.". Part of the deal with Acme includes setting aside parcels of land from Plot X for the construction of low- and medium-cost housing. This area is known as the Acme Subdivision (Acme Sub). Because of the local demographics, the majority of Acme Sub homeowners and renters, mainly heads of households, will be employed by Acme. Four years ago the Zilch River flooded to 100-year severity.

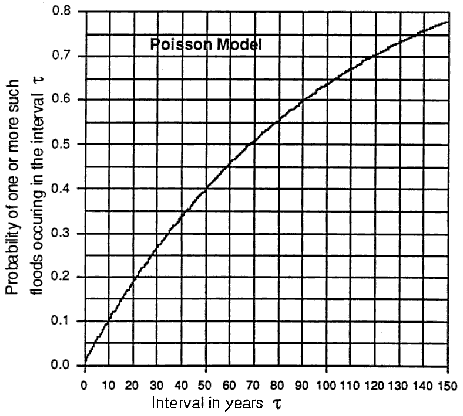
1. Assuming that the floods may be modeled as a Poisson process, prepare a plot of the probability of one or more 100-year flood occurring in any time interval from 1 year to 150 years.
2. Prepare an oral presentation, not to exceed 20 minutes, to explain the results of part (a) to a general audience. Assume an average general education level of 12th grade, but only 5th grade competence in mathematics. Consider in turn, each of the mutually exclusive scenarios below in (b1), (b2), and (b3).
   1. Suppose you make the presentation out of public service considerations only, i.e. you have no financial interest in the project and will not be affected directly by the decision to build or not to build the plant.
   2. Suppose you make the presentation as a paid consulting engineer for the local entities seeking to attract Acme to build the plant.
   3. Suppose you make the presentation as a paid consulting engineer for "Save Our River," a citizen's group seeking to block construction of the Acme plant.
   4. Comment on any differences in the presentations in (bl), (b2), and (b3).
   5. Consider your answer to (b) in light of the ABET Code of Ethics, or an ethics code of any engineering society. What guidance, if any, does the code provide that may be applicable here.
3. It is pointed out that the Zilch flooded to the 100-year level only four years ago. It is thus argued by some that "...we don't have to worry about another flood for 96 years." Comment on this assertion. Be sure to support your comments with appropriate mathematics.
4. Based on the fact that the Zilch flooded to the 100-year level four years ago, compute the probability of such a flood occurring again in the next ten years. Repeat for the interval of the next 30 years.
5. A person interested in buying a house in Acme Sub comes to you for help. They want you to determine which of two options they should take, based only on cost considerations. (Assume all non-stated matters are equal for either option. Further assume that only the 100-year flood will destroy the house of Option A, and that it will not damage the house of Option B. Either house will be ready for occupancy in two years.) Ignore the present-worth-of-money concept. Use 30 years as the analysis period, beginning two years from now.

Option A

Purchase a home in Acme Sub with a 30-year mortgage payment of $250/month. Payments include all taxes, insurance, etc., except flood insurance. Flood insurance costs $300/year and is "locked in" at that rate for 30 years. In the event of flood, the flood insurance payment will cover new house construction costs only. Household goods are not covered and are valued at $10,000 (excludes vehicles), and are assumed destroyed in the event of a flood.

Option B

Purchase a home identical to that of Option A, but built on a lot which is well above the flood plain. The 30-year mortgage payment is $300/month (includes same items as Option A). The differential cost (Option B relative to Option A) of commuting to work by the homeowners is $45/month. (f) It is proposed to build flood control works such as dams, levees, diversion canals, etc. to mitigate flood risk and damage. Assume that the construction of these works would transform the 100-year flood plain into a 500-year event. The cost summary for the proposed flood control project, and estimates for flood losses resulting from either the 100-year or 500-year flood, are given in Table 1. Use a 30-year study period, ignoring the time-value of capital to determine if the flood control project is cost-justified. (g) If your solution in (f) indicates that the flood control project is not justified, at what study time period is the project justified?

Back to Top

Solutions

1. Here the Poisson process is described by:
   

   In the problem of interest p(n) is the probability of precisely n occurrences of the 100 year flood in the time interval z. λ the parameter is the rate at which the phenomenon occurs, i.e. 1/100 years. λ for the Poisson process the mean is τ. The desired plot may be obtained by taking τ as the discrete variable: τ = 1, 2, ...150 years, and summing:

1. Although τ is shown above is a discrete variable we plot it as a continuous one: P(τ) = 1 - exp(-λ τ) over the range of interest.

2. A difficult task! Perhaps appealing to intuition (carefully!) can set the background needed.
3. One cannot attribute memory to the river! It doesn't "know" that it flooded four years ago. The events are said to be statistically independent and we may use the plot above to determine the probability of one or more floods (in addition to the flood of four years ago) in any interval of τ years beginning from the present. The ideas here are discussed in most texts on introductory probability theory.
4. Use P(τ) = 1 - exp(λ τ). For τ = 10 years, P(10) = 1 - exp[-(0.01)(10)] = 0.095. For τ = 30 years, P(30) = 1 - exp[-(0.01)(30)] = 0.259.
5. The expectation is the probable loss due to flooding. It is the product of the mean for the case of τ = 30 years and the dollar loss per event (flood), which was given as $10k.

   Option A

   Mortgage: M = ($250/month)(12 mo/yr)(30 yr) = $90,000 Flood insurance: F = ($300 yr)(30 yr) = $9,000 Uninsured losses from flood: L = (λ τ)($10,000) = [(0.01)(30)][$10,000] = $3,000 30 year cost: S = M + F + L = $102,000

   Option B

   Mortgage: M = ($300/month)(12 mo/yr)(30 yr) = $108,000 Differential commute cost: C = ($45/month)(12 mo/yr)(30 yr) = $16,200 30 year cost: S = M + C = $124,200 Therefore, Option A is better. Note that the analysis ignores effects floods have on the quality of life, in terms of trauma, disruption, etc.

6. The sum of costs for the project is: $45M + $5.0(30) = $195M. The sum of damage costs is: $408M. The Poisson-process mean value for 30 years interval, for 500 year flood-risk is: 30/500 = 0.060; resulting in an expected loss of: (0.060)($408M) = $24.3M. Therefore, if the project is built, the expected cost is: S = $195M + $24.3M = $219.3 (with project) Without building the project, the expected loss (30/100)($408M) = $122.4M (without project) Therefore, the flood control project is not justified.
7. Find T to satisfy: 45 + 5T + (T/500)(408) s (T/100)(408) (in $M) T = -25.9 years Thus, building the flood control works is not feasible for any study interval. Note that the time value of capital was ignored. Plot for solution to part (a).

Back to Top